エクセルで対角線の長さの計算をする方法【直角三角形の底辺と高さから斜辺を求める】

エクセルはデータ解析・管理を行うツールとして非常に機能が高く、上手く使いこなせると業務を大幅に効率化できるため、その扱いに慣れておくといいです。

ただ機能が充実しているあまり初心者にとっては処理方法がよくわからないことも多いといえます。

例えばエクセルにて対角線の長さを計算したり、直角三角形の底辺と高さから斜辺の長さを求めていくにはどうすればいいのか理解していますか。

ここでは「エクセルにて対角線の長さ（2次元・3次元）や直角三角形における底辺と高さから斜辺の長さを求める方法」について解説していきます。

エクセルにおいて対角線の長さを求める方法【2次元・3次元】

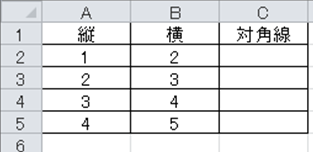
それでは以下のサンプルデータのような長方形の対角線の長さを、エクセルを用いて計算しみましょう。

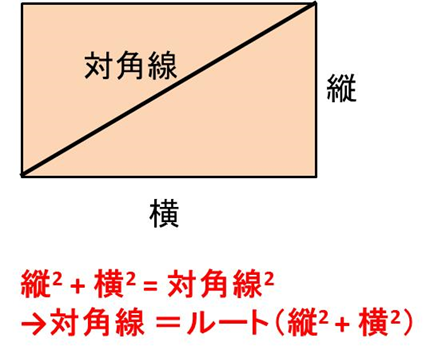
長方形の対角線の長さを求めるには、三平方の定理（縦^2+横^2=対角線^2）を式変形した対角線 ＝ルート（縦² + 横²）という計算式にて処理していきます。

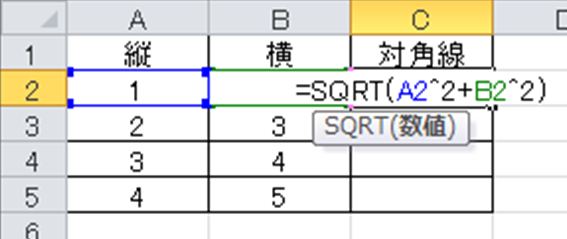
具体的にエクセルにて対角線を計算するには今回では=SQRT(A2^2+B2^2)という数式を任意のセルに入れるといいです。

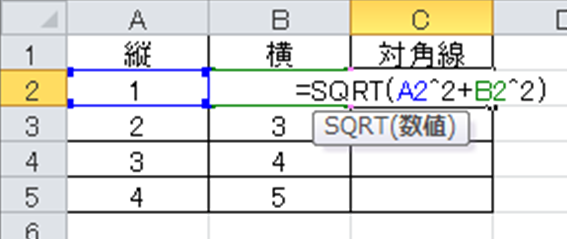
上の関数の意味を解説します。

SQRT関数とはルートをつける関数であり、

にて処理できます。今回では中身が縦の2乗と横の2乗の和なので、上のような数式になるわけです。

ENTERにて計算を確定後にオートフィル（セルの右下にカーソルを合わせると出る十字をドラッグ&ドロップ）によって一括計算しましょう。

すると以下のように長方形における対角線の長さを求めることができました。

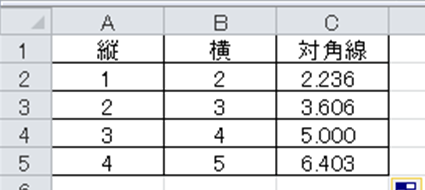
なお、正方形でも同じように対角線の長さを求めることができますが、正方形では縦＝横の長さであり、対角線の長さ＝1辺の長さ×ルート2でも求められますので、適宜処理するといいです。

直角三角形における斜辺の長さを底辺と高さから計算する場合も同じ

上では長方形の対角線を求める方法として処理していますが「対角線を直角三角形の斜辺」と見た場合でも全く同じ計算によって直角三角形の斜辺の長さを高さと底辺の数値から求められます。結局は呼び方が違うだけで、意味は同じだからです。

データの名前を縦→高さ、横→底辺、対角線→斜辺と置きかえ、同じ数式を入れていけば底辺と高さの数値から直角三角形の斜辺が求められるのです。

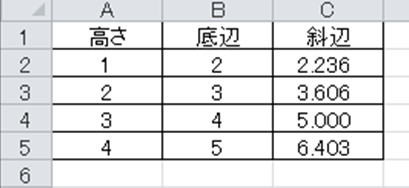
上の2次元における対角線の計算式と併せて理解しておくといいです。

エクセルで3次元（直方体）の対角線の長さを計算する方法

続いて、以下のサンプルデータを用いてエクセルにて3次元（直方体）での対角線の長さを計算する方法について確認していきます。

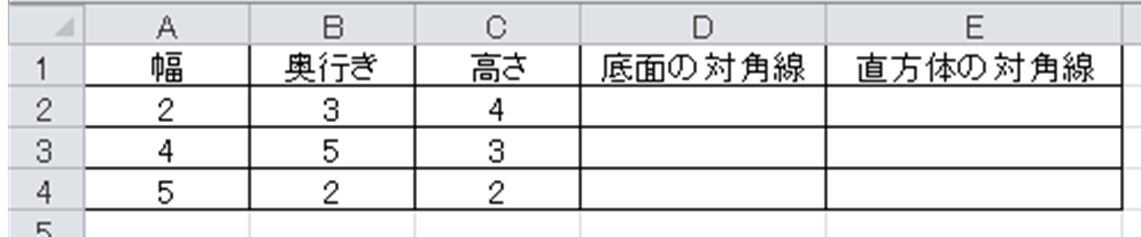
エクセルにて3次元の対角線の長さを求めるには、そもそもの直方体での対角線の計算方法を理解しておく必要があります。

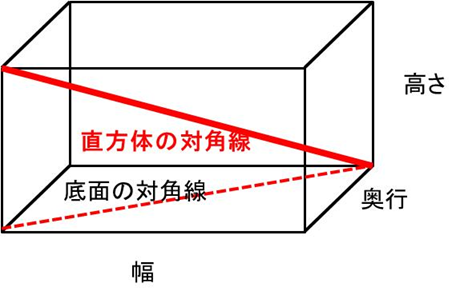
直方体の対角線を計算するには

といいです。

これをエクセルで表現するには、=SQRT(A2^2+B2^2)と任意のセルに入れるといいです。

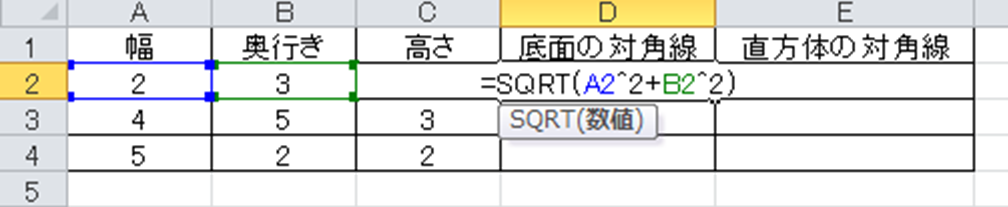
ENTERにて決定後にオートフィルにて、一括で底面の対角線を求めることができます。

続いて 直方体の対角線の長さ＝ルート（底面の対角線の2乗 + 高さの2乗）の計算式を元にし=SQRT(C2^2+D2^2)と入力しましょう。

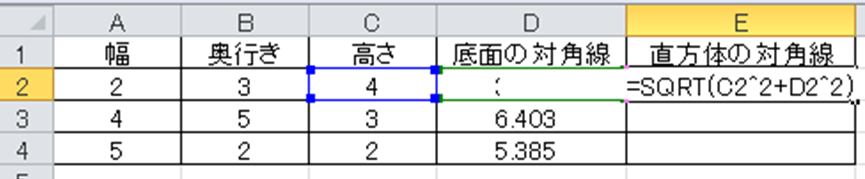
再度処理確定後にオートフィルでコピーします。

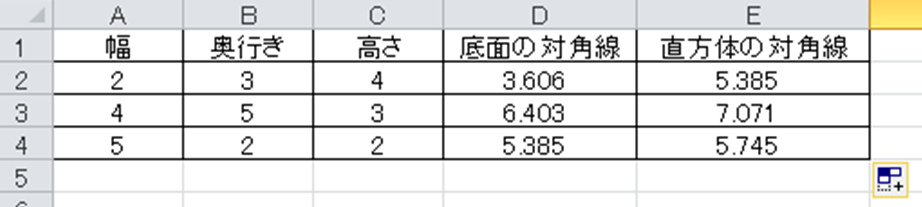
このようにしてエクセルでの直方体の対角線を計算する方法が完了となるのです。

まとめ　エクセルで直角三角形の底辺と高さから斜辺を求める方法【対角線の長さの計算をする方法】

ここでは、エクセルにて対角線の長さを計算したり、直角三角形の底辺と高さから斜辺の長さを求めていく方法について確認しました。

基本的には各定義に従って計算式をエクセルにて処理していくとよく、ルートをつけるためにSQRT関数を使うといいです。

エクセルでのさまざまな処理方法を身につけ、日々の業務を効率化していきましょう。