エクセルはデータ解析・管理を行うツールとして非常に機能が高く、上手く使いこなせると業務を大幅に効率化できるため、その扱いに慣れておくといいです。
ただ機能が充実しているあまり初心者にとっては処理方法がよくわからないことも多いといえます。
例えばエクセルにて「角度の単位のラジアンと度数の変換方法」「三角関数(sin・cos・tan)と逆三角関数(sin-1・cos-1・tan-1)の計算」「正弦波や余弦波のグラフを描く方法」等について理解していますか。
ここではこれら三角関数に関係する一連の関数やグラフの描き方について解説していきます。
エクセルにてラジアン(rad)と度(dgree)の変換を行う方法【角度の関数】
エクセルにておいて三角関数やその逆関数の計算を行う際には、その角度の単位として度数方(単位が度:degree)ではなく、弧度法(ラジアン:rad)を使うのが基本です。
そのため、まずはこれら「度とラジアンの変換」をエクセルにて行う方法を確認します。
度(degree)からラジアン(rad)への変換【RADIANS関数と角度】
以下のサンプルデータを用いて度数からラジアンに角度を変換するには、RADIANS関数と使用するといいです。
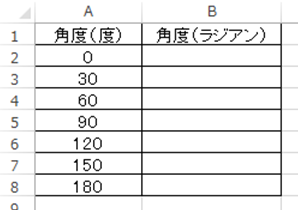
と入れるとよく、今回では=RADIANS(A2)と任意のセルに入力しましょう。
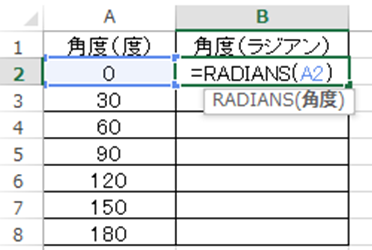
ENTERにてラジアンの角度に変換後、オートフィル(セルの右下に出る十字をドラッグ&ドロップ)によって、一括処理していきましょう。
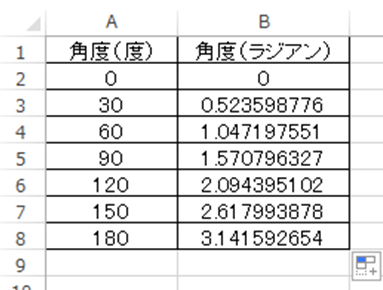
ここで、180度=πラジアンという本来の角度とラジアンの計算式が一致していることがわかるのです。
度(degree)からラジアン(rad)への変換【DEGREES関数と角度】
今度は逆に、上の数値を元にラジアンから度に変換してみましょう。
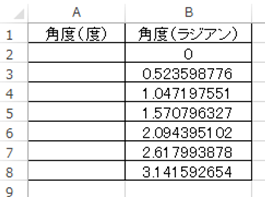
この時にはDEGREES関数を使用し
と入力しましょう。今回では=RADIANS(B2)と任意のセルに入れるといいです。
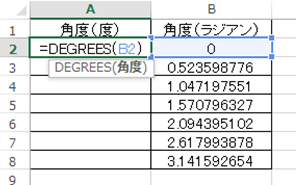
こちらでも処理確定後にオートフィルで一気に単位が度数の角度を変換しましょう。
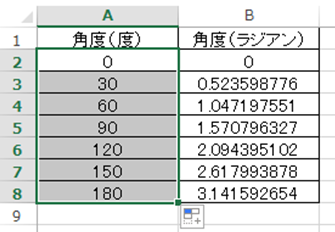
これでエクセルでのradからdegree単位の角度への変換が完了します。
エクセルにて三角関数(sin・cos・tan)の数値計算を行う方法
続いて上の知識を元に、三角関数の(sin(サイン)・cos(コサイン)・tan(タンジェント))の変換を行っていきましょう。
sin(サイン)の数値を求める【sin関数】
エクセルにてsin(サイン)の数値を計算していくには、sin関数を用いるといいです。
sin関数では
と入力する必要があります。今回ではセルに=SIN(B2)と入れるといいです。
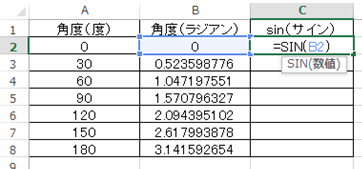
決定後にオートフィルにて三角関数のサインの数値を出力していきます。
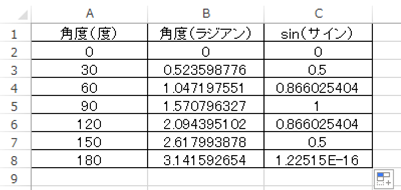
このようにしてエクセルでのsinの計算が完了となります。
なお後に解説しますが、sin(180度)の数値が0になっていないのを確認できますが、これは割り切れない数の円周率を使っているために近似値となることから、どうしても誤差が生じるものなのです。(ほぼ0ではあります)。
cos(コサイン)の数値を求める【COS関数】
今度はエクセルでのcosの数値計算も行ってみましょう。
エクセルにてcos(コサイン)の数値を計算していくには、cos関数を用いるといいです。
cos関数は
と入力すればよく、今回ではセルに=COS(B2)と入れます。
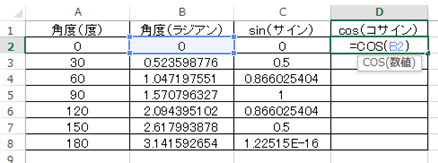
上と同様にENTERにて処理確定後に、オートフィルをかけましょう。
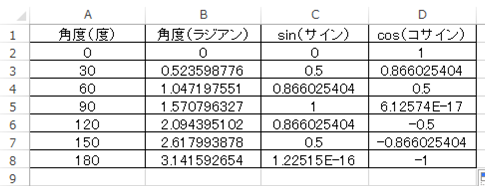
このようにしてエクセルのでcosの数値計算ができます。
tan(タンジェント)の数値を求める【tan関数】
さらにはエクセルでのtanの数値計算も行ってみましょう。
エクセルにてtan(タンジェント)の数値を計算していくには、tan関数を用いるといいです。
tan関数は
と入力すればよく、今回ではセルに=TAN(B2)と入れます。
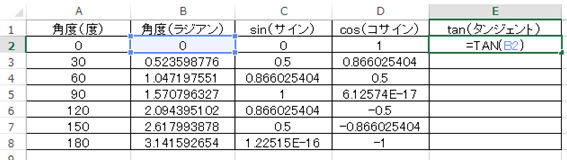
上と同様にENTERにて処理確定後に、オートフィルをかけましょう。
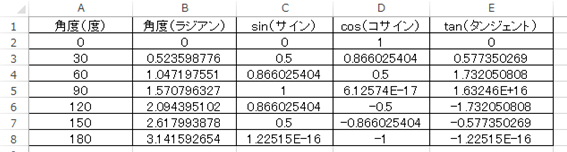
このようにしてエクセルのでtanの数値計算ができます。
エクセルにて逆三角関数(sin-1、cos-1,tan-1)の計算をする方法
続いてエクセルにおける逆三角関数(sin-1、cos-1、tan-1)の計算方法についても確認していきます。
三角関数では角度から各々の数値を取得していたわけですが、逆三角関数では数値から角度を計算することができるのです。
sin-1(アークサイン)の数値を求める【sin-1の読み方とASIN関数】
まずはエクセルにてsin-1の計算方法について確認していきます。なお。このsin-1の読み方としては、サインインバース、サインの逆関数、アークサインなどが代表的です。
具体的にはエクセルのASIN関数を使うとよく
と入れることで、ラジアン表記の角度を返します。度数に変換したい場合には出力値をさらに変換しましょう。
今回ではセルに=ASIN(C2)と入れるといいです。
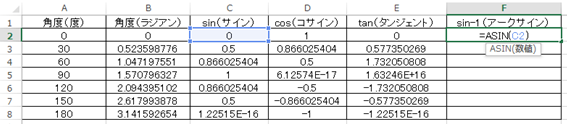
決定後にオートフィルにて逆三角関数のサインインバースの数値を出力していきます。
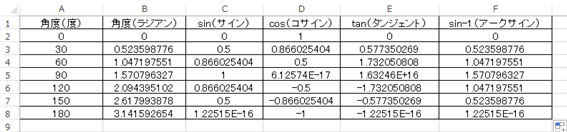
このようにしてエクセルでのsin-1の計算が完了となります。
なおB列の角度と比較すると途中までは同じものの、一部が違う値を返しています。これはASIN関数では基本的に同じ数値の場合は角度の小さいものを出力するものだからです(sinの数値に対応する角度は2つあることもあるため)
cos-1(アークコサイン)の数値を求める【cos-1の読み方とACOS関数】
続いてエクセルにてcos-1の計算方法について確認していきます。なお。このcos-1の読み方としては、コサインインバース、コサインの逆関数、アークコサインなどが代表的です。
具体的にエクセルでACOS関数を使うとよく
と入れることで、ラジアン表記の角度を返します。度数に変換したい場合には出力値をさらに変換しましょう。
今回ではセルに=ACOS(D2)と入れるといいです。

決定後にオートフィルにて逆三角関数のコサインインバースの数値を出力していきます。

このようにしてエクセルでcos-1の計算が完了となります。
なおB列の角度と比較すると同じになっていることがわかります。これはコサインの数値は0~180度では値が一つしかないために、その解(角度)をそのまま出力しているためです。
tan-1(アークタンジェント)の数値を求める【tan-1の読み方とATAN関数】
続いてエクセルにてtan-1の計算方法について確認していきます。なお。このtan-1の読み方としては、タンジェントインバース、タンジェントの逆関数、アークタンジェントなどが代表的です。
具体的にエクセルではATAN関数を使うとよく
と入れることで、ラジアン表記の角度を返します。度数に変換したい場合には出力値をさらに変換しましょう。
今回ではセルに=ATAN(E2)と入れるといいです。

決定後にオートフィルにて逆三角関数のタンジェントインバースの数値を出力していきます。

このようにしてエクセルでtan-1の計算が完了となります。
なおタンジェントインバースは途中までB列の角度同じですが、一部が違う数値になっています。これはサインインバースと同様に同じtanの数値を満たす角度が複数あることが理由であり、-の数値を優先して出力するためにこのような状況になっているのです。
エクセルにて正弦波(サインカーブ)のグラフを描く方法【sinカーブの作成】
上のように三角関数(sin・cos・tan)と逆三角関数(sin-1・cos-1・tan-1)の基礎的な数値計算ができるわけですが、この応用として正弦波(サインカーブ)のグラフを作成していきましょう。
正弦波(sinx)のグラフの作り方としては、横軸に角度(任意の単位)、縦軸にsinの数値を用います。
今回は角度(x)として度数表示の数値を使用し、10度刻みかつ範囲を0~720度としてみましょう。
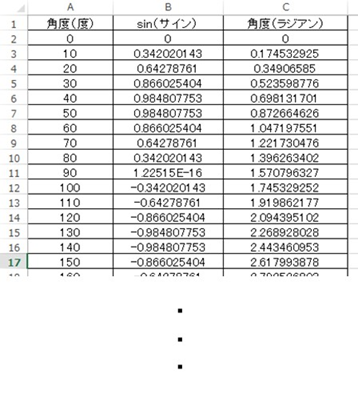
上の要領でまず度数表記の角度をラジアンに変換後、sinの数値をSIN関数より求めておきます。この時
・xに対応する角度(度)と
・yに対応するsin(サイン)の数値
がA,B列になるよう整理するとグラフ化しやすいです。
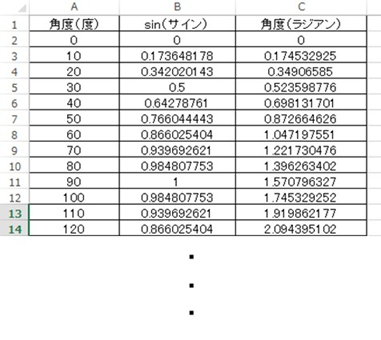
続いて正弦波のグラフを作成するためのxとyの数値全体を選択後、上の挿入タブ、散布図、平滑線と指定しましょう。
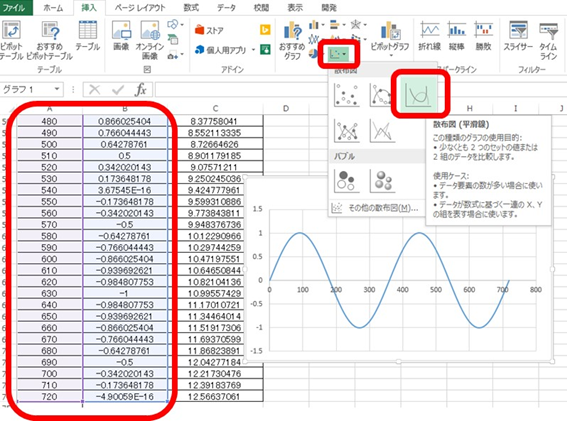
ENTERにて決定するだけで正弦波のグラフを描くことができるのです。
体裁を整えるために、x軸をクリック後に表示される右のウィンドウにて目盛の数値を90とすると正弦波のグラフがより見やすくなります。
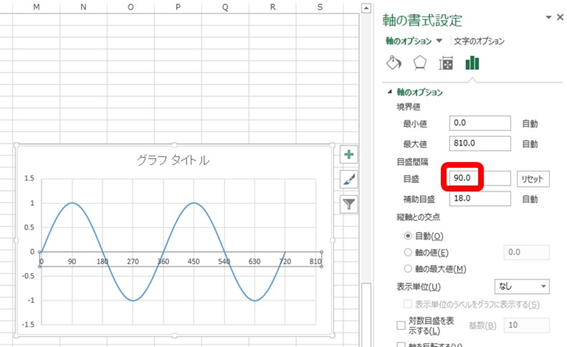
すると以下のように正弦波(サインカーブ)のグラフが描けました。
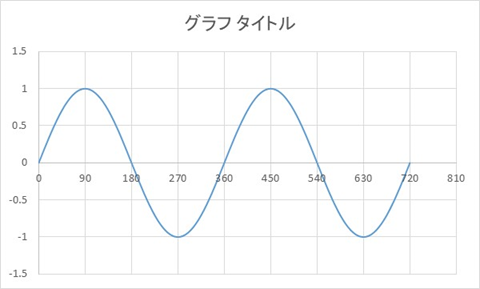
正弦波のグラフにて正弦波の周期を変える【sin2xのグラフ】
続いては、正弦波のグラフとして周期を変化させたsin2xのグラフを描いてみましょう。
y=sin2xと周期が変わった正弦波のグラフを描くには上にてyの数値の中身を変更させる必要があります。
sin2xのグラフとするには、元のサインのセルの入力の数式を=SIN(2*C2)と角度を2倍したものに置き換えるといいです。

後はオートフィルにて一括でy=sin2xの数値にすると周期が変わった正弦波のグラフ用データに変換できました。
sin2xと周期が変わったサインカーブのグラフを確認しますと、以下のようになります。
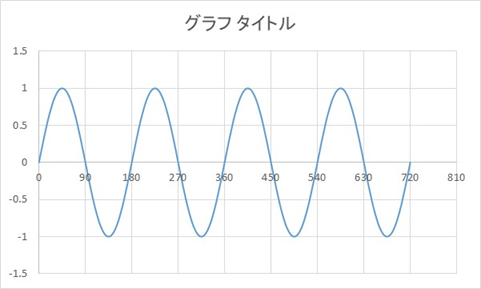
周期が半分になっていることが確認できますね。
コメント